روش برنز-فیشر یا تانژانت تتا(tanɵ)
روش برنز-فیشر(B-F) یا تانژانت تتا(ɵ) در آمار، همانند آزمون ولچ برای بررسی برابری میانگینهای μ۱ و μ۲ دو جمعیت نرمال مستقل است که در آن واریانسهای σ۲۱ و σ۲۲ ناشناخته و نامشخص هستند. مسئله زمانی به وجود می آید که نسبت واریانس جمعیت نیز ناشناخته باشد.
برنز و فیشر رابطه زیر را برای توزیع احتمال پیشنهاد کرده اند:

که x1 و x2 میانگین نمونه ها و s۱ و s۲ انحرافهای معیار هستند. فیشر این توزیع را با نادیده گرفتن تغییرات تصادفی اندازههای نسبی انحرافات استاندارد تقریب زد. پارامتر C در آزمون فیشر به صورت زیر تعریف میشود:
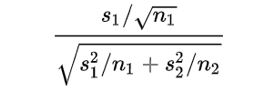
راه حل فیشر بحث برانگیز بود، زیرا این ویژگی را نداشت که اگر میانگینها واقعا برابر باشند، فرضیه میانگینهای برابر با احتمال α رد شود.
با این حال، نمونههای مستقل از دو جمعیت دو پارامتری (غیر از حالت عادی) در بسیاری از موقعیتها به وجود میآیند. مشکل این است که برابری دو پارامتر مکان (یا برخی از پارامترهای مشابه) را زمانی که پارامترهای پراکندگی (یا برخی پارامترهای مشابه) ناشناخته و احتمالاً متفاوت هستند، آزمایش کنیم. این مشکلات مشابه مشکل قدیمی Behrens-Fisher است.
قبل از سال ۲۰۱۴ مطلب زیادی در مورد حل مشکلاتی مشابه با Behrens-Fisher نوشته نشده بود. برخی از مشکلات مشابه با مسئلهی B-F که اخیراً به آنها پرداخته شده است، عبارتند از: (الف) آزمایش برابری دو میانگین دوجملهای منفی در حضور پارامترهای پراکندگی نابرابر. (ب) آزمایش برابری پارامترهای مقیاس دو توزیع ویبول(Weibull) در حضور پارامترهای شکلی نابرابر. (ج) آزمایش برابری دو نسبت دو جملهای بتا در حضور پارامترهای پراکندگی نابرابر.
وقتی حجم نمونه کوچک است، آزمون t(t-test) دو نمونه (T۱) با درجه آزادی ولچ(Welch) و برای اندازههای نمونه بزرگ (N = n۱ +n۲ > 30) آزمون آماری نرمال استاندارد (TN) توسط کتابهای درسی استاندارد(مانند کتاب آمار و طراحی آزمایشها در رشتههای علوم و مهندسی نوشته دکتر شهره فاطمی) توصیه میشود.
شواهد زیادی به نفع ترجیح Welch T۱ نسبت به سایر روش ها نشان داده شده است. برای مثال، برای مسئله استاندارد BF ببینید(این مثالها را در منابعی که در پایان مطلب ذکر شدهاند میتوانید ببینید). اخیراً یک روش مبتنی بر jackknife و یک روش محاسباتی فشرده برای مشکل BF توسعه داده شده است. با این حال، هیچ مطالعه سیستماتیکی تاکنون برای تعیین اندازه کلی نمونه مورد نیاز که در آن تقریب نرمال آماره TN کار میکند، انجام نشده است.
برای BF استاندارد و برخی از مشکلات مشابه با آن، عملکرد یک رویکرد جدید مونت کارلو، بوت استرپ(bootstrap) و همتایان همرتبه بررسی شدهاند. مطالعه اخیر نشان میدهد که Welch T۱ در برخی موقعیتهای غیرعادی، مانند نمونههایی از دو جمعیت دوجملهای منفی، خوب عمل میکند.
مطالعات اخیر نشان میدهد که Welch T۱ در برخی موقعیتهای غیرعادی، مانند نمونههایی از دو جمعیت دوجملهای منفی، خوب عمل میکند. همراه با برخی رویههای دیگر، عملکرد Welch T۱ و رویکرد جدید مونت کارلو برای نمونههایی از جامعهی نرمال، دو مدل گسسته (شمارش دادهها و دادهها به شکل نسبتها) و یک مدل بقا برای طیف گستردهای از فضاهای پارامتری مورد را بررسی میکنند تا مقایسهی میانگینها برای واریانسهایی که یکسان یا بسیار متفاوت هستند را منعکس کنند.
هدف ثانویه بررسی و پاسخ به یک سوال است: آیا اندازهی یکسان برای همه مناسب است یا به عبارت دیگر آزمون t با درجه آزادی تصحیح ولچ به اندازه کافی برای آنالوگهای مسئلهی BF قوی است و چه اندازه نمونه برای تقریب طبیعی آماری TN مناسب است.
در نظر بگیرید ، . . .، یک نمونه تصادفی از یک جامعه باشد، i = 1, 2. حال، در نظر بگیرید که ، . . .، یک تحقق نمونهی متناظر با میانگین و واریانس است. اگر نمونهها از جمعیتهای عادی با میانگین μ۱ و μ۲ و واریانسهای ناشناخته و احتمالاً نابرابر σ۲۱ و σ۲۲ باشند، داریم:
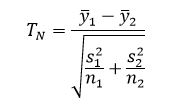
به طور مجانبی معمولاً با میانگین ۰ و واریانس ۱ توزیع میشود که هر دو n۱ و n۲ به اندازه کافی بزرگ باشند. این موضوع در بسیاری از کتاب های درسی در مقطع کارشناسی در رشته آمار ریاضی بیان شده است. با این حال، زمانی که اندازههای نمونه n۱ و n۲ کوچکتر باشند، توزیع TN که از این پس با T۱ نشان داده میشود، تقریباً به صورت t-Student با درجههای آزادی توزیع میشود.
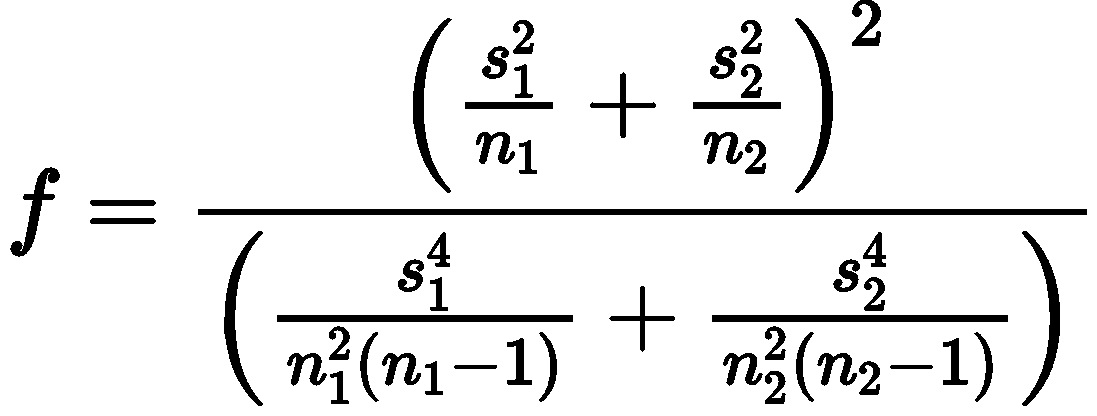
برخی از منابع با استفاده از شبیه سازی نشان دادند که آماره ی

ممکن است به آمارهی T۱ اولویت داشته باشد، باشد زیرا اولی سطح اسمی(nominal level) را بهتر از آماره بعدی حفظ میکند.
در این مقاله با روش برنز – فیشر آشنا شدیم. این روش طراحی آزمایش بسیار پرکاربرد است. برای آشنایی با سایر موضات مرتبط قسمت گلوپ پلاس را مطالعه کنید.
منابع
(۳ مورد اول مربوط به مثالهای ذکر شده هستند)
Best, D. J. and Rayner J. C. W. (1987). Welch’s Approximate Solution for the
Behrens-Fisher Problem. Technometrics ۲۹, ۲, ۲۰۵{۲۱۰.
Derrick, B. and Toher, D. and White, P. (2016). Why Welchs test is Type
I error robust. The Quantitative Methods in Psychology ۱۲, ۱, ۳۰{۳۸
Paul, S. R. (1992). Comment on Best and Rayner (1987). Technometrics ۳۴, ۲,
۲۴۹{۲۵۰.
Algina, J. and Oshima, T. C. and Lin, W.-Y. (1994). Type I error rates for
Welchs test and Jamess second-order test under nonnormality and inequality of
variance when there are two groups, Journal of Educational Statistics 19, 3, 275{
Brensike, J. F., Kelsey, S. F., Passamani, E. R., Fisher, M. R., Richardson, J. M., Loh, I. K., Stone, N. J., Aldrich, R. F., Battaglini, J. W., Moriarty, D. J., Myrianthopoulos, M. B., Detre, K. M., Epstein, S. E., Levy, R. I. (1982). National Heart, Lung, and Blood Institute Type II coronary intervention study: design, methods, and baseline characteristics. Control Clin. Trials 3,2 91{111.
چنانچه در حوزه کاری خود به مشکلی برخورد کردهاید و در جستجوی فرد و یا شرکتهای توانمند برای حل مشکلتان هستید می توانید با عضویت در سامانه گلوپ و ثبت مشکل خود با این افراد و شرکت ها ارتباط برقرار کنید.
برای مشاهده مطالب بیشتر به گلوپ پلاس مراجعه فرمایید.